ボンドグラフの基礎:10
ボンドグラフとブロック線図
ボンドグラフもブロック線図もいずれもシステムを表現するものです。トップページのシステム表現に機械系モデル、電気回路モデル、油圧回路モデルのシステムの表現を示しました。いずれの場合も素子固有の表現と素子を結合する保存則あるいは連続式によりシステム表現が可能になっています。ブロック線図表現とボンドグラフ表現に簡単なシステムについて2つを対比して示してあります。ボンドグラフではシステム内部の素子の接続関係が表現され、ブロック線図では変数相互の関係を表現しています。いずれもシステムの数式表現と対比すると直接対応していることが読み取れます。従って、ボンドグラフとブロック線図は因果関係(causal)を有するという意味では同一とみなすことができます。 しかし、いずれの表現もシステムを動的システムの観点から抽象化していますので、システムの細部の情報、例えば変数の基準点などの情報は捨てられているといえます。このような情報は回路図や流体系のスケマティクスによらなければなりません。
ここで、ブロック線図表現の特徴を整理しておきましょう。
- ブロック線図では信号を線で、矢によってその向きを、そしてシステムまたはその素子をブロックで表します。
- ブロック線図で用いられる要素には4つあります。図に示します。向きのある信号線、ブロック、分岐、加え合せです。ブロックには特性式が記入されます。

- 向きのある信号線は情報をしめすもので、エネルギー伝達を意味しません。ブロックには入力と出力があり、入力に基づき出力の計算がされます。
- ブロックは変数相互の関係を示すだけであり、モデルの数式表現には対応しますが、システムの物理表現に直接対応するものではありません。
物理モデルからボンドグラフの作成
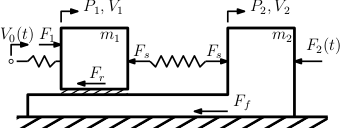 左図は移動台に載せられた移動する小物体です。このシステムをボンドグラフで表現してみましょう。
移動台には右方からF2(t)の力が作用します。小物体の質量はm1、
移動台の質量はm2です。移動台と台上のm1の間には摩擦力Frが作用します。移動台と床の間の摩擦力はFfとします。移動台と台上の小物体はばねで結合されていて、ばね力はFsとします。台上物体の左方にもばねがあり、ばねは左方から速度V0(t)を生じるように
押されています。簡単のため摩擦力は粘性摩擦のみとします。P1、P2はそれぞれm1、m2の運動量とします。従って、P1=m1⋅V1、P2=m2⋅V2です。
左図は移動台に載せられた移動する小物体です。このシステムをボンドグラフで表現してみましょう。
移動台には右方からF2(t)の力が作用します。小物体の質量はm1、
移動台の質量はm2です。移動台と台上のm1の間には摩擦力Frが作用します。移動台と床の間の摩擦力はFfとします。移動台と台上の小物体はばねで結合されていて、ばね力はFsとします。台上物体の左方にもばねがあり、ばねは左方から速度V0(t)を生じるように
押されています。簡単のため摩擦力は粘性摩擦のみとします。P1、P2はそれぞれm1、m2の運動量とします。従って、P1=m1⋅V1、P2=m2⋅V2です。
ボンドグラフで考えるにはエフォート×フロー=エネルギーの流れを考える必要があります。明らかに、力×速度=F×v=[N]⋅[m/s]=[J/s] 。m1 に対するばねの力F1の着力点の速度V1はV0(t)と異なり、力はF1ですので、着力点が0接点です。m1には力F1、Fr、Fsが作用し、速度V1を生じます。m1は1接点です。m1とm2の中間のばねはm1、m2の相対速度 により伸縮し、力Fsを生じます。相対速度を生じる点は0接点です。小物体m1に働く摩擦Fr はm1とm2の相対速度に比例します。ここも0接点です。台に働く力はばねFs、摩擦力Fr、Ff、外力F2(t)であり、これにより速度V2を生じます。従って、m2は1接点です。摩擦力Ffは床との速度V2により決まります。
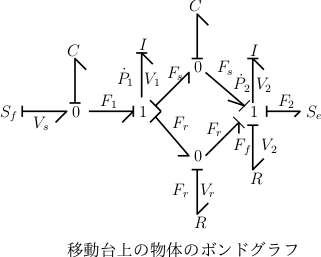
以上をボンドグラフで表現すると、左図のようになります。
| 前のページ<< | >>次のページ |
