トップ 1 BGSP V2 がリリースされました
2023年9月1日に BGSPの次世代ヴァージョンを公開いたしました。 BGSP V2 では GUI 機能と偏微分方式の表示機能が追加され、よりユーザフレンドリーなソフトウェアへと進化しております。 使い方およびインストール方法などについては、下記からご覧ください。
ダウンロード
BGSP V2のダウンロード
こちらからzipファイルをダウンロードし解凍してください。
インストール方法
zipファイル内のDocumentsフォルダに含まれる、「BGSPの設定方法(240109).pdf」をご参照ください。
使い方
zipファイル内のDocumentsフォルダに含まれる、「BGSPマニュアル20240106.pdf」をご参照ください。
編集後記
BGSP(Bond Graph Simulation Program)は、1985 年に、日本機械学会研究協力部会,RC68油空圧システム省エネルギー調査研究分科会の成果として報告されたものである。BGSPは、当時、通商産業省工業技術院機械技術研究所(現、産業技術総合研究所)で、幸田武久博士(機械技研→京都大学、故人)、中田毅博士(機械技研→東京電機大学、名誉教授)を中心に製作され、一般に公開(1988年)されているシミュレーションプログラムである。その後に、(社)日本油空圧学会(現、一般社団法人、日本フルードパワーシステム学会)のOHC-Sim委員会(桜井康雄博士(足利大学))で、油圧記号のアイコン化とマッチさせて油空圧分野でより使いやすくするためにプログラムの修正なども行われた。
BGSPには、ボンドグラフで表されるシステム変数間の因果関係に着目した、簡単な数式処理を用いることにより、
- ① システム状態方程式が、関数表現形で自動的に導出されてシミュレーションが行われ、
- ② 非線形特性を持つ要素を含むシステムが簡単に取り扱え、
- ③ フィードバック特性を持つような素子の特性が使用者により自由に定義でき、
- ④ システム動特性のほかに使用者が定義するエネルギー効率などの特性値が計算できる、
などの特徴がある。プログラムはFORTRAN 77言語で記述されており、パソコン上でも使用でき、他のシステムへの移植も簡単である。
上記の紹介文は、J.U. Thoma & 須田信英 著、ボンドグラフによるシミュレーション、コロナ社(1996年)、の該当箇所をほとんど原文のまま、ただし、誤った記述を修正するなどを行って後に掲載したものです。BGSPの特徴がよく明示されています。
その後、BGSPはC言語、C++言語でも書き下されて、BGSP Ver2は双方の言語での使用が可能です。また、当初のBGSP(便宜上、これをVer.1と呼ぶ)では、システム・ボンドグラフ構造の入力形式がプログラム・ベースであったために、使用方法が煩雑であり一般化しませんでした。そこで、富岡弘毅博士(九州工業大学、博士修了、故人)、田中和博博士(九州工業大学、名誉教授)によりGUIを利用して画面上でボンドグラフ構造の入力が可能となるように修正変更がなされました。
その後、肥後寛氏(九州工業大学)の協力を得て、プログラムのデバッグが行われ修正された箇所があります。またいくつかの便利な機能が付加、拡充されました。そこで、BGSP Ver.2の特徴を纏めると、上記の①②③④に下記の項目を付け加えることとなります。
- ⑤ 入力素子に実験値入力が可能であり、
- ⑥ 変数のチェック機能が充実され、
- ⑦ 何にでも利用できる便利なグローバル変数XX(i)が用意されたことで、再帰型ループの解消が容易に可能となっており、
- ⑧ システム・ボンドグラフより状態方程式の導出が可能である。
BGSP Ver.2は各種の機能が整うまでに時間が掛かりましたが、GUIは15年前にほぼ完成しており、それを利用したシステム動特性解析はこれまでに200例を超えます。
これらの結果の中で不合理な結果を得ることはなかったと考えています。したがって、BGSP Ver.2を信頼して利用していただければ幸いと考えています。
しかし残念ながら、気が付かなかった間違いもあるものと思われますので、もしお気づきの点があれば是非ご連絡を願いいたします。
ユーザーフォーラム
simtecでは、ソフトウェアの使い方や、モデリングのディスカッションができるユーザフォーラムを立ち上げました。
ユーザーフォーラムを参照ください。
トップ 2
このホームページは、BGSP(Ver. 1)の時代より長期にわたり維持されてきているものであり、BGSP V2をオープンすることにより仲間を増やしながら、この手法の便利さを理解していただければ考え方の系統化に役立つと考え、引き続きボンドグラフの普及を目指すものです。
トップ2 以下の内容は、BGSP(V1)の頃から、ボンドグラフのモデリングとシミュレーションに基づいて記述されている内容です。この中の例題のシミュレーションプログラムの一部で、システム・ボンドグラフの構造が書式として表現されている箇所がそのBGSP(V1)に立脚しているものであり、その点のみがBGSP(V2)と異なる点です。使用するプログラムに依らないボンドグラフのモデリングに関する項目や話題については、今でも重要でかつ役立つものであることには変わりはありません。 その点をご理解の上、このホームページを楽しんでいただければ幸いと考えます。また、新たにユーザーフォーラムなるものを立ち上げて、最近の研究や開発に関する資料や情報を随時掲載していきたいと考えております。以後、よろしくお願いいたします
ボンドグラフによるシミュレーション
工学的システムを実現するには品質(Q)、コスト(C)、スケジュール(D)の制約が課せられます。どれほど素晴らしいアイデアであってもQCDの目標を満足できなければ絵に書いた餅であり、アイデア倒れに終わる可能性があります。そうならないためには、設計段階での十分な検討が必要です。ところが、最近の製品は例えばメカトロニクスにあるように複合的な技術分野にまたがるものが多くなっています。このため、複数の専門家から構成される技術チームを必要とすることになります。
ここで専門分野の異なる技術チームには、コミュニケーションをどうとるかの問題点があります。電気・電子技術者は目に見えない電気・電子の振る舞いを理解するすべを心得ていますし、機械技術者は平面的な図面から具体的な物を3次元的に理解することができます。しかし、お互いのイメージづくりの文化が異なりますから、専門用語で話しあう限り相互理解は不十分になりがちです。油圧、空圧、熱、磁気等さまざまな分野で同様のことが予想されます。
そこで、相互理解にはまず、システムの振る舞いを平易な言葉で説明することが求められます。この時、モデルの概念が重要となります。モデルとはシステムを実現するために関連のある要素を総合して目的をもって表現されたものです。現実の世界は複雑ですが、設計の目的ではあらゆる構成要素を記述する必要はないからです。
しかし、複合的技術分野にまたがるシステム・モデルを言葉だけで説明するのは現実には困難です。数式によるシステムの記述、機械図面、油圧回路図、あるいは電気回路図、部品図、模型など言葉を補うモデルが必要になります。これらの補助情報は一般的に専門性が高くなり、コミュニケーションを阻害します。
そこで、グラフあるいは図解による説明が登場します。図解による表現は相互理解を進め、アイデアを生む機会を生じます。さらにより進んだ手段としてシミュレーションが取り上げられます。シミュレーションとはシステムを可能な限り数式もしくは実験データの表などで表現し、コンピュータ計算により動的、静的なふるまいを示すものです。システムをほぼ任意の点で観測し、動的のみならず効率などの静的な特性までも知ることができるのです。
グラフを用いたシステム・モデルの表示法にはさまざまな方法があり、ブロック線図、リニアグラフ、シグナルフロー図、ボンドグラフなどがあります。自動制御システムではブロック線図、シグナルフロー図がしばしば用いられますが、これらはシステム内の入出力、あるいは内部状態を示す信号の関係を示すものであり、システムを構成する要素の特性と要素の接続関係を示す基本式により表わされます。ボンドグラフはやや異なり、システム内の要素のエネルギー伝達に着目するもので、システム内の部品の相互関係を図式により把握しやすい特徴があります。エネルギー伝達の観点からは、機械、電気、磁気、熱、油圧等さまざまな技術分野のシステムを統一的に表現できます。ボンドグラフによれば、複合的システムの理解が容易にできるのです。
設計には試行錯誤が避けられませんが、システムのふるまいを具体的なデータに基づいて把握できれば、専門分野の異なる技術者にもシステムの具体的なイメージが明らかとなり、客観的評価が可能になります。モデルを可能な限り視覚化し、かつ、定量的解析を可能にすることこそ、効率的設計には必要不可欠と申せましょう。 ボンドグラフによるシミュレーションは視覚化、定量的解析、複合的技術分野の統一的表現など設計の効率化の強力なツールとなり得るものです。
システムの表現
簡単なモデルを取り上げ、異なる技術分野のシステムがさまざまに表現されることを示します。
機械系モデル
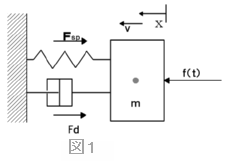
図1は減衰振動機械系モデルです。記号は次のとおりです。

式は次の(1)~(4)のとおりです。式(1)~(3)はシステムを構成する要素の特性式であり、(4)は要素を結びつけるシステムの関係式です(ダランベールの定理)。
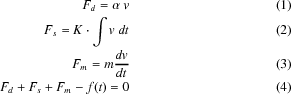
電気回路モデル
図2は減衰振動電気回路モデルです。記号は次のとおりです。

式は次の(5)~(8)のとおりです。式(5)~(7)はシステムを構成する要素の特性式であり、式(8)は要素を結びつけるシステムの関係式です(キルヒホッフの第2法則)。
油圧回路モデル
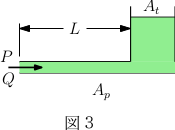
図3は油圧回路モデルです。記号は次のとおりです。

この油圧回路では右方のタンクに左方から圧力Pで下方のパイプから流体が流れ込みます。パイプ流量はQとします。流体は非圧縮性とし、パイプ内の流れは層流とします。式は次の(9)~(12)のとおりです。式(9)~(11)はシステムを構成する要素の特性式であり、式(12)は要素を結びつけるシステムの関係式です。。
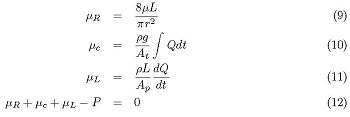
式(9)はパイプを通る層流の抵抗を示すHagen-Poiseuilleの式です。式(10)はタンク底面の圧力を示します。式(11)はパイプ内を通る流体の慣性力を示します。式(12)はすべての力のつり合いを示します。
数学的表現
機械モデル(式1~4)と電気回路モデル(式5~8)、油圧回路モデル(式9~12)を比較すると次の表のように対応がとれます。数学的表現としては同形であることが分かります。
| 機械モデル | f | v | m | K | |
|---|---|---|---|---|---|
| 電気回路モデル | e | i | L | R | 1/C |
| 油圧回路モデル | P | Q |
f(t),e(t)を入力としてv(t),i(t)を出力とする式は次のようになります。
機械系モデルでは次のようになります。
![]()
電気系モデルでは次のようになります。
![]()
油圧系モデルでは次のようになります。
![]()
![]()
2次式で表現できるような簡単なシステムの場合には、このように理解は容易です。しかし、複雑なシステムを数式のみで表現するのは、コミュニケーションをとるには大変不都合なものとなります。また、計算は数式ごとに工夫しなくてはなりませんから、決して容易ではありません。理解を容易にする図式表現法として、広く用いられるものにブロック線図があります。
ブロック線図表現とボンドグラフ表現
ブロック線図による表現
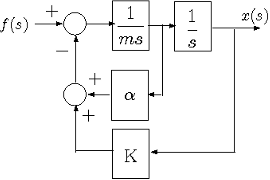
実際、直ちに2次式で表現できるシステムは実務ではめったに存在しません。複雑なシステムの表現方法としてブロック線図がよく用いられます。上の機械モデルでは左図のようになります。システム要素はラプラス変換形で表現しなくてはなりません。2次系では簡単に描けますが、高次系となり、かつ非線形要素が入ると必ずしも容易ではありません。 ブロック線図で表現すると、MATLABあるいはSCILABにより計算できますし、グラフによる表示も容易にできる利点があります。図の表現は(1)~(3)式をそのままブロック線図として表現したものです。ブロック線図は着目した信号の流れとして表現されます。ブロック線図を導くには定式化が前提となります。しかしながら、ブロック線図からシステム内の具体的な対象が何なのかを把握することは困難です。
ボンドグラフによる表現
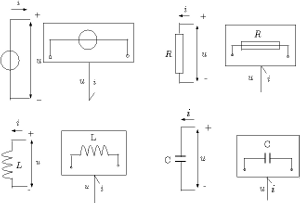
パワーポートと要素
左図はこれまで示したRLC電気回路モデルの各要素をボンドグラフで表現したものです。機械モデルも同一の形で表現できます。どの要素も共通変数として
があります。それぞれの要素の入力パワー
ですから、結合素子として"1"ジャンクションを用いると左下図のようになります。これはフローである
が共通でありパワーの合計が0という意味です。エフォートが等しく、フローが異なる場合(キルヒホッフの第一法則)では、結合の記号として"0"ジャンクションを用います。
これをまとめ、システムのボンドグラフとしたものを右下図に示します。たいへん簡潔なグラフとなっているのがおわかりでしょう。かつ、システムの要素であるR、L、C、入力源がそのまま把握できます。番号のついた片矢印はボンドといい、エネルギーの方向を示します。片矢印の一方にはストロークとよばれる棒がついていますが、後で説明します。SEは外力である入力信号、LはインダクタンスCはキャパシタンスRは抵抗を表します。なお、ボンドグラフの基礎を御覧下さい。機械モデルでも同型となります。このモデルで便宜上SE、R、C、Lのすべてのデータは1であるとし、計算してみると、最下図のようになります。確かに減衰振動であることがわかります。
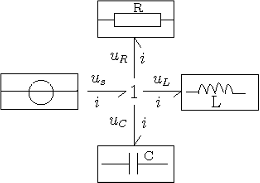
電気回路要素とボンドグラフ |
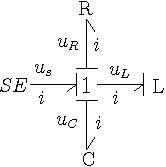
ボンドグラフ本来の記法 |
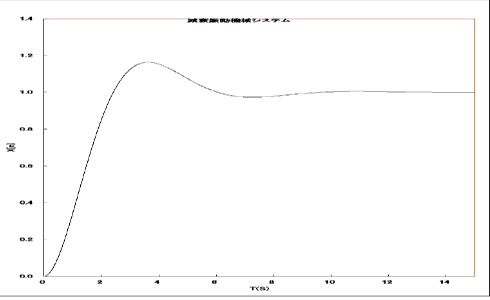
ボンドグラフ・シミュレーション結果
ボンドグラフの実務への応用
ボンドグラフは複合的な技術システムのシミュレーションを行うのに強力なツールとなります。しかし、実務に利用するためには次のようなことが課題となります。
- 参考書
邦文の参考書としては[1]が唯一のものです。[1]はボンドグラフの基礎的事項からかなり高度の話題まで包含しています。なにぶん碩学の著書であるだけに、さりげなく書かれた事項にもかなりの技術的素養を要求する場合があり、初学者にとって必ずしも入りやすくはありません。また、刊行以来20年となり、古書市場でも高額で、書籍の入手自体が難しい難点があります。
このサイトでは、演習問題の解説と各種のトピックにより、必ずしも[1]を参照しなくてもボンドグラフの理解が可能なように努めます。 - プログラム
ボンドグラフを基礎とする高機能ソフトとして、最近はAMESIMなどが登場しています。しかし、AMESIMは非常に高額なソフトでこれを使用できる環境をお持ちの方は少ないでしょう。また、AMESIMは高機能である反面、モデルの数学的表現は不明確になるおそれがあります。小規模のシステムでは、むしろボンドグラフにより表現するほうが物理モデルとの対応が明確で、思考を整理するには便利です。
ボンドグラフの習得と応用には、なによりも実際の問題についてボンドグラフを描き、計算することによりボンドグラフに慣れることが必要です。[1]には21題の例題が掲載され、ボンドグラフ・モデル及びTUTSIMのコードが載っています。ボンドグラフ学習者にとり、まさに好適の教科書となり得るものです。ところがTUTSIMの後継とされる20-SimはTUTSIMに完全互換とされますが、実際にはTUTSIMのコードをそのまま入力することはできません。20-SimはViewerについては無償で使用することができ、簡単な問題についてはViewerでシミュレーションできます。(2015年10月からpersonal useに限り、100ユーロ、邦貨約13,000円と大幅に値下げされ、入手が容易になりました。H27.10.1追記)
[1]p198に簡単に紹介されているBGSPは京都大学の幸田教授が開発し、その後(社)日本油空圧学会において改良が加えられたプログラムですが、このサイトではシミュレーションプログラムのページからダウンロードできます(BGSPのインストールマニュアル)。ボンドグラフの学習と応用のためにはほぼ十分な能力を有しています。 - 学習と応用
ボンドグラフの学習と応用のため、本サイトでは[1]の例題について解説を加えながら、BGSPと20-Simを併用し、実際にシミュレーションすることにより、シミュレーションの演習とすることとしました。BGSPあるいは20-Simのコードまで載せましたので、読者は実際にボンドグラフのコードを書き、解答を比較することができます。演習に加え応用のための様々な話題を取り上げます。さらにコード作成においては工夫が必要な場合があるのでTipsとして話題としました。 これにより実務においてボンドグラフ・シミュレーションを行うために本サイトが役立つことを願っています。(20-Simの入手が容易になりましたので、すべての例題について20-Simのコードを付記することにします。しばらく時間がかかりますが、ご容赦願います。H28.5.5)
