簡単な油圧回路

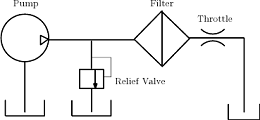
左図に示す簡単な油圧システムについてボンドグラフによるシミュレーションを行います。ほぼ文献[5]によりますが、別解法を付け加えています。

理想的定流量源であるポンプからの流れは、フィルタを通り、絞りから外部に流出します。フィルタに至る管路には安全弁が設けられていて、管路の圧力を制御します。絞りの部分ではフィルタを通過後の圧力と絞りを出た後との圧力差により流量が決まります。管路では粘性により圧力損失が生じます。管路とフィルタの容積効果により圧力が決まります。各要素の特性式はつぎのようになります。

ボンドグラフは2つに分割され、ダミー素子で接続しています。理由は直接接続すると解不能となるからです。ボンドグラフから数式モデルを求めるためには、状態方程式表現が必要とされますが、素子間の因果関係の結合によっては代数ループを生じる場合があり、解が得られなくなります。[1]6章をご覧ください。

  1. ポンプ

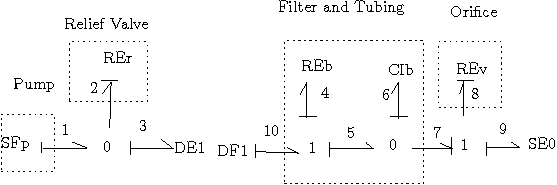
    2. ポンプは定流量源SFpで表され、

    F=F0
F0:ポンプの吐き出し流量

    の特性式となります。

  2. 安全弁

    3. 特性式は次のようになります。特性式を表現するプログラムはコードをご覧ください。

    　安全弁から出る流量[m^3/s]
    　許容限度圧力[Pa]
    　安全弁の感知圧力[Pa]
    　安全弁の抵抗係数[Pa・s/m^3]
  3. 管路の圧力損失

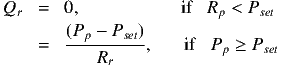    4. 次のとおりです。

    　圧力損失[Pa]
    　管路流量[m3/s]
    　抵抗係数[Pa・s/m^3]
  4. 絞り

    5. オリフィスの式で表します。

    　絞りにおける圧力効果[Pa]
    　吐出し流量[m^3/s]
    　管路抵抗係数[Pa・s/m^3]
  5. 管路とフィルタの容積効果

    6. 管路とフィルタの容積効果はC-素子でモデル化され、特性式は次のようになります。

    　ポンプ系全体の吐出し圧力[Pa]
    　管路とフィルタの容積/体積弾性係数[m^3/Pa]
    　吐出し圧力初期値[Pa]

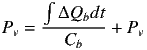    パラメータとして次のような値を仮定します。

    : [m^3/Pa]
    : :[Pas/m^3]
    :[m^3/Pa]
    :[Pas/m^3]
    :[Pas/m^3]
    :[m^3/s]

    出力項として、次のようにします。

    FLFL:安全弁のエネルギー損失
    FLRV:管路とフィルタ部分のエネルギー損失
    P-PR:ポンプからの吐出圧力
    F-out:絞りからの流量:

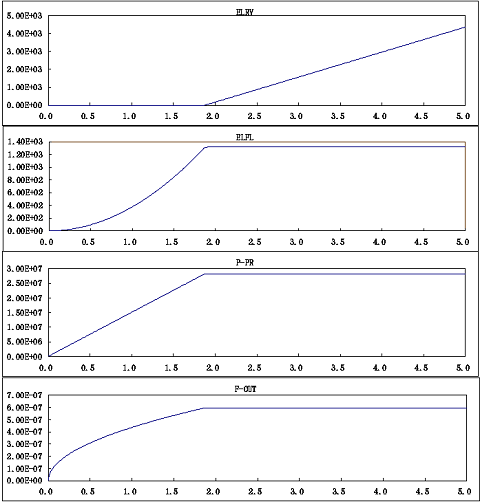
シミュレーション結果

シミュレーションの結果を下図に示します。安全弁のエネルギー損失ELRVはボンド2に流れるエネルギー量で表されますから、'BC: ELRV EN3'の形でボンド特性値を用いて表現されます。ポンプの吐き出し圧力P-PRと絞りからの流量F-OUTのそれぞれボンド2のエフォートEF2とボンド8のフローFL8で指定されています。管路やフィルタでのエネルギーロスはその部分への流入エネルギーEN10と流出エネルギーEN7の差ですから、FLFL=EN10-EN7の形で計算されます。ボンド特性値EN10とEN7を用いますので、'FB; X11 EN10'と’FB: X12 EN7'で変数が定義されて、'OP=X11-X12'で出力項が表現されています。このようにユーザーが計算したい出力項も自由に表現できます。コードをご覧ください。

解法：２ ダミーボンドを使用しない解法

解１では、理想流量源から直ちにリリーフ弁につながっています。、実際にはポンプ容積があり、このようなことにはなりません。そこで、ポンプ容積と配管容積を仮定し、モデルを修正します。下図が修正したボンドグラフです。配管圧力損失を示すREbのボンドは方向が反対になります。これは因果関係があうようにするためです。しかし、これは物理的現象の解釈の問題でもあり、別に恣意的にモデルを組み立てているわけではありません。そこで、解法１で示した式は次のように修正されます。

:
管路流量
圧力損失
:抵抗係数
ポンプ容積圧力効果

ポンプ容積圧力効果は管路とフィルタの容積効果と同様としますが、値は小さくとっています。ボンドグラフは下図のようになります。

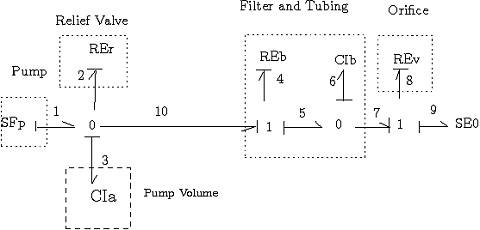
シミュレーション結果は解法１とほとんど同じですので省略します。