シミュレーションの演習

GS14:シリコン基板の熱伝導

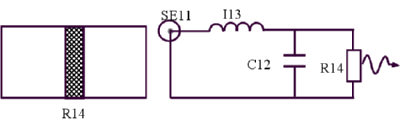左図はシリコン基板の横断面と電気回路図を示します。SE11は電源であり、基盤には右の回路図で示すようにインダクタンスとキャパシタンスが存在します。R14は負荷とみなされる抵抗値です。この問題は電気回路と熱回路が接続されているため、ボンドグラフ表現の上でも興味深いものです。R14で電気的エネルギーが熱エネルギーに変換されます。上図でR14から右に延びる曲線は熱エネルギーの放射を示します。
ボンドグラフの表現上では電気回路、機械回路、油圧回路、熱力学などさまざまな技術分野で統一的表現が可能です。熱力学上でもエフォートを絶対温度T[K]、フローをエントロピー流速[J/K/s]とすることにより、エフォート×フロー=[J/s]となります。しかし、熱回路について言えば熱抵抗[K/W]、熱容量[J/K]を用い、エフォートを絶対温度T[K]、フローを熱流量[J/s]として表現すれば、熱回路の表現と計算が容易になる利点があります。この場合、フローが既にパワーになっていますから、エフォート×フローは意味のない量となります。これを擬似ボンドグラフといいます。フローにエントロピー流速を用いる場合を真のボンドグラフといいます。この場合の計算は偏微分方程式を解くことになり、表現も計算もかなり困難です。電気回路の部分のボンドグラフと熱回路の擬似ボンドグラフを接続し、電気回路と擬似ボンドグラフによる熱回路をシミュレーションすることがここでの問題の要です。

RS要素の導入

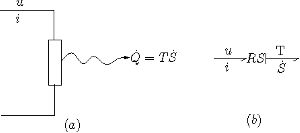ここで、シリコン基板は熱的な閉鎖空間にあるとします。抵抗に流入した電気エネルギーは熱エネルギーに変換されますが、全エネルギーの流れとしては不変です。流入する電流は電気回路単独では決定されません。なぜなら、温度が変化すれば、抵抗による熱放散も変化し、流入電流も変化するからです。もし、抵抗の存在する空間が無限の熱容量を有する場合には、流入電力は熱放散には無関係となり、単独の抵抗素子として差し支えありません。熱エネルギーを考慮すると、(a)図、及び上図の抵抗R14は1ポートだけの単純な抵抗素子ではなく、熱ポートを有する特殊な抵抗素子とみなされます。Thoma教授はこれを”RS素子”と名づけ、次の関係式で表現しました。ボンドグラフでは上の(b)図のように表現されます。

ここで、uは入力電圧、iは電流、Tは絶対温度[K]、はエントロピー流量[J/s/K]です。

RS要素を計算するボンドグラフ

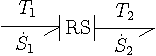上の図(b)のRS要素の計算方法を検討します。RS要素の入出力のいずれでも絶対温度、エントロピー流量がありますから、図(b)は左のように表現されます。 RS要素の入口と出口でエネルギーは保存されますから、次の式が成り立ちます。

また、

ですから、RS要素を計算するボンドグラフは次の図のようになります。R12により計算される(u,i)からエントロピー流量を計算し、SF121によりフローを発生させ、温度T1を掛け、さらにT2で割ることにより、上記のRSの計算が実現できるのです。この図はあくまで真のボンドグラフの計算式であり、擬似ボンドグラフはこれを応用して次項のようになります。なお、ここでSFの入力信号はR12のフローであることに注意してください。

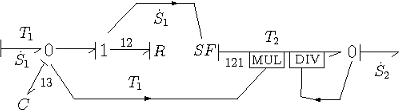
シリコン基板の熱伝導の擬似ボンドグラフ

このボンドグラフは[1]でシリコン基板の熱伝導に対する電気回路と擬似ボンドグラフを示しています。RS要素の左側が電気回路のボンドグラフであり、インダクタンスI13とキャパシタンスC12が見えます。RS要素の右側が熱回路の擬似ボンドグラフであり、基板材料の熱容量と熱伝導を擬似ボンドグラフで表現しています。RS要素の右側のエフォートは絶対温度T[K]であり、フローはエントロピー流束[J/s/K]ですが、これにRS要素の左側の絶対温度T1を掛けて熱流速[J/s]としています。従って、RS要素の右側のフローはとなります。熱流束は次の式で表現されます。

熱流束はフーリエの式を用いると、次のようにも表現されます。

ここで、K=熱伝導率[J/K]です。 ここから疑似ボンドグラフで表現されるエフォートは両端の温度差であることが分かります。なお、ここでの説明はやや便宜的で、Thoma教授が[1]で実際には役に立つが, 美しくはないといっているとおりですが、より厳密な説明は[2]p46にありますのでご覧ください。

シミュレーション

さて、問題はシミュレーションのためには"RS"要素の計算をしなくてはなりませんが、どうすればよいのでしょうか。BGSPではできません。20-Simでは任意の要素を定義できることになっているので、可能です。

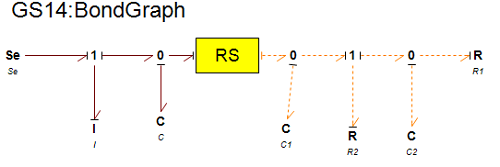
図は要素RSを定義した場合のボンドグラフです。RS要素の左側は電気回路を示し、右側は熱回路です。RS要素の右側：点線で示されている部分が疑似ボンドグラフで表現されています。エフォートが絶対温度[K]、フローは熱流束[J/s]を意味します。なお、RS要素を定義するためには、20-Simのサブモデル定義によるセーブ、さらにインターフェース・エディターを用いて、入力が電気システム、出力が疑似ボンドグラフの熱回路であることを指示しなくてはなりません。また、アイコンについてもアイコン・エディターにより定義します。なお、熱容量C1、C2及び熱抵抗R1、R2の算出根拠の文献は示されていません。

RS要素の式は次のようになります。

parameters
real R_ref=0.063 {ohm};//electric resistance
real alpha=0.3;
real T1_ref=0.0 {K};
variables
	real R {ohm},T1 {K},u {W};
equations
	R=R_ref*(1+alpha*(T1.T-T1_ref));
	u.i=u.u/R;
	T1.dQ=u.u*u.i;

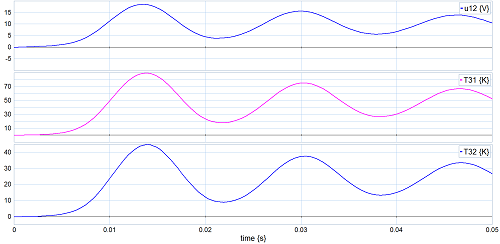
シミュレーションの結果を下に示します。[1]とかなり類似しています。ただし、[1]とは常数を変更しています。u12の応答に減衰はあるものの減衰量は少なくなっています。u112が振動するのはRSの温度上昇・減少により抵抗値が増大/減少し、結果として発生熱量も減少/増大するからです。温度T31及びT33は最高値がそれぞれ90[K],45[K]ですから[1]よりもやや高くなっています。alphaなる係数は実験値と考えられるのでこの値を調節すれば、異なる応答になります。あるいは他の設定値に相違があるのかもしれません。